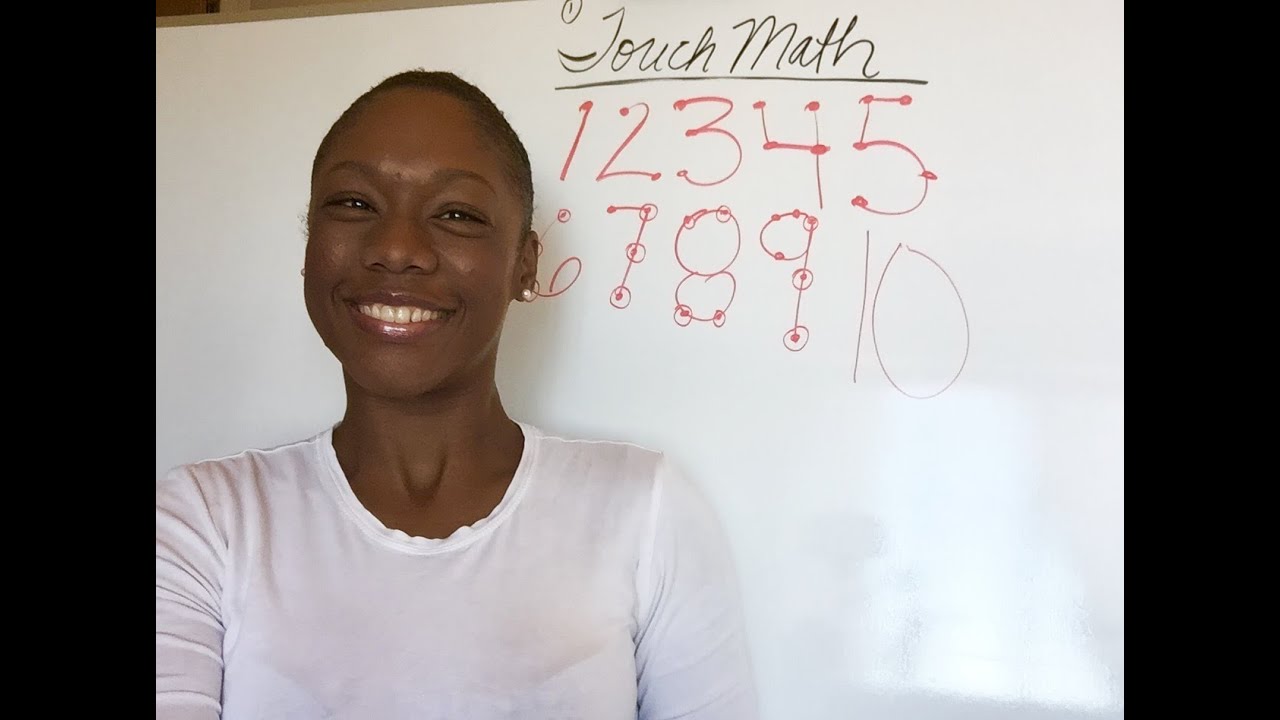Film ve Animasyon
For the full MightyOwl learning experience, check out more activities, worksheets and quizzes on our website:
👉 https://MIGHTYOWL.COM/
Hop on over to help Will and his froggy friend count to 100! Learning to count up to 100 is a rite of passage in #Kindergarten, and easily mastered with patterns. Using a hundreds chart and color coordination, students will have no problem #countingto100 on their own after this video!
Key words: counting, hundreds chart
Aligned with Common Core State Standard - Math
K.CC.A.1 - Counting & Cardinality
Know number names and the count sequence: Count to 100 by ones and by tens.
In this tutorial I explain the super easy concept of touch math. I explain how it's used to add and subtract numbers which keeps you from counting on your fingers. Remember where the dots are so the next time you see a number, you’ll only see dots.
You can download notes from this tutorial and practice problems at:
https://www.neenareedknows.com/
How to Divide Numbers Using Long Division? Basic Math Review
For Sharpie Markers you can visit their online stores:
Lazada: https://www.lazada.com.ph/shop/sharpie?path=index.htm&lang=en&pageTypeId=1
Shopee: https://shopee.ph/sharpie.ph
Visit our new fb page: www.facebook.com/MathTutorialsforFree/
for business inquiries: teachergonmath@gmail.com
Civil Service Examination Reviewer Playlist:
Solving Age Problems PART 1 - Civil Service Exam
https://youtu.be/FZmZUaet3Ig
How to Solve Age Problems (Part 2) - Civil Service Exam - LET Exam
https://youtu.be/738Xx0qfX2E
Number Series - Math Reviewer - Civil Service Exam and LET
https://youtu.be/TfvN_NSbfdk
Order of Operations - PEMDAS - Civil Service Exam & LET Reviewer
https://youtu.be/pfnctEEWuuM
How to Solve Word Problems in Ratio and Proportion
https://www.youtube.com/watch?v=TrunSSuYrAg
How to Solve Number Problems? | Civil Service Exam - LET
https://youtu.be/95dGkfHGWT0
Percentage Hacks! How to Get the Percentage of a Number?
https://youtu.be/h8yfFXq-pCI
This is educational video for grade 6 to check their Math knowledge.
It includes math concept which will help you in your exams. Can you pass 6th grade Quiz?
#6thgrademathtest, #graderQuiz
Grade 2 Math Glenda Santiago W6
A motivational song for Math Learners.
Learning Math is fun.
God bless!
123 numbers matching | math worksheet for lkg ukg class | toppo kids
Match numbers with their spelling | class lkg ukg math worksheet for kids | toppo kids
Content cover in this video -
123 numbers matching worksheet
math worksheet for nursery class
math worksheet for lkg class
math worksheet for ukg
math worksheets for kindergarten
math worksheets
math worksheet for kids
math worksheet for class 1
About this Video -
In this video we are going to learn about numbers name 1 to 20 with spelling | This video is made for kids. Which will help them learn numbers 1 to 20. Visual in the form of colorful things is a treat for the kids, toddlers, babies, children loves Colours hence we have used colourful numbers and things to create this nunber video we produce very simple and fun loving straight forward video for childrens, babies and toddlers so that learning become easy. Our 2D animation videos have lots of colors so that kids get engrossed and learn from the educational videos we produce.
Parents, teachers, kindergarten schools, preschools, babies, kids will surely enjoy the video..
Our some other educational playlist links -
Preschool + Nursery Full Course: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
LKG Full Course: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
Learn Alphabet: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
English - LKG / UKG.: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
English Worksheets for kindergarten.: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
English dictation for kids.: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
Learn हिन्दी Alphabet: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
हिन्दी Worksheets for kindergarten: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
Learn Numbers: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
Names- Fruits, Vegetables, Animals etc..: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
Gk worksheets for kindergarten: https://www.youtube.com/playli....st?list=PLU7y7WxCttw
Hope you like the content we create.
Please don't forget to like, share and subscribe to our channel - TOPPO KIDS.
#ToppoKids
#kidslearningvideos
#lkgmath
#ukgclass
#numbername
#LEARNNUMBER1TO20WITHENGLISHSPELLINGFORKIDS
#numbersong
#countings
#learnnumbers
#1to10
#kindergarten
#preschoollearningvideosfor3yearolds
#learningvideosforkids #kidseducationalvideos
Welcome to Types of Angles with Mr. J! Need help with the different types of angles? You're in the right place!
Whether you're just starting out, or need a quick refresher, this is the video for you if you're looking for help with different types of angles. Mr. J will go through an example of an acute angle, an obtuse angle, a straight angle, a reflex angle, and a right angle and each type of angle will be explained.
About Math with Mr. J: This channel offers instructional videos that are directly aligned with math standards. Teachers, parents/guardians, and students from around the world have used this channel to help with math content in many different ways. All material is absolutely free. #MathWithMrJ
Click Here to Subscribe to the Greatest Math Channel On Earth: https://goo.gl/XHTrfY
Follow Mr. J on Twitter: @MrJMath5
Email: math5.mrj@gmail.com
Music: https://www.bensound.com/royalty-free-music
Hopefully this video is what you're looking for when it comes to different types of angles.
Have a great rest of your day and thanks again for watching! ✌️✌️✌️
✅ Thanks to Aloud, this video has been dubbed into Spanish and Portuguese. #DubbedWithAloud
English
This video has been dubbed into Spanish (United States) and Portuguese (Brazil) using an artificial voice via https://aloud.area120.google.com to increase accessibility. You can change the audio track language in the Settings menu.
Spanish
Este video ha sido doblado al español con voz artificial con https://aloud.area120.google.com para aumentar la accesibilidad. Puede cambiar el idioma de la pista de audio en el menú Configuración.
Portuguese
Este vídeo foi dublado para o português usando uma voz artificial via https://aloud.area120.google.com para melhorar sua acessibilidade. Você pode alterar o idioma do áudio no menu Configurações.
TabletClass Math:
https://tcmathacademy.com/
Introduction to Calculus, easy to understand for those that want to know what Calculus is. For more math help to include math lessons, practice problems and math tutorials check out my full math help program at https://tcmathacademy.com/
Math Notes:
Pre-Algebra Notes: https://tabletclass-math.creat....or-spring.com/listin
Algebra Notes: https://tabletclass-math.creat....or-spring.com/listin
Geometry Notes: https://tabletclass-math.creat....or-spring.com/listin
Algebra 2 / Trig Notes: https://tabletclass-math.creat....or-spring.com/listin
How to become a math genius !
If you are a student and learning Maths and want to know how genius people look at a math problem then you are on a right place because in this video I am going to share with you the mindset of every successful mathematician ,who created history in Math . This will make the boring math super interesting for you. so apply this method .........
video on how to learn anything-https://www.youtube.com/watch?v=l5icegYOOE4&t=7s
I wish you all the very best for your further math studies!
If you liked the video subscribe to our youtube channel !
Watch This video also-https://www.youtube.com/watch?v=iruIt_QwGRc
WE also have a facebook group to discuss math of over 8k people ! link below
https://www.facebook.com/groups/1350780458373702/
like us on our facebook page!=https://www.facebook.com/MathO....genius-1542565051449
-~-~~-~~~-~~-~-
do not forget to watch "How To Get 90%+ Marks In class 12th Boards(2018)✔️ (Easiest way!) By mathOgenius"
https://www.youtube.com/watch?v=OOF23fXuW-Y
-~-~~-~~~-~~-~-
#mathOgenius
How to calculate the hours and minutes between two events.
Greater than Less than Equal to for kids | Comparison of numbers | Math Grade 1
This video aims at teaching Greater than, Less than and Equal to concepts in Math. This fun video will help them understand the comparison of numbers in an easy way.
Background images and alligator images source:
http://www.vecteezy.com/free vector
Watch more videos on
English Grammar
https://www.youtube.com/playli....st?list=PLmMD9No9Nct
Hindi matrayen
https://www.youtube.com/playli....st?list=PLmMD9No9Nct
Phonics Lessons
https://www.youtube.com/playli....st?list=PLmMD9No9Nct
English Poems
https://www.youtube.com/playli....st?list=PLmMD9No9Nct
Hindi Bal Kavitayen
https://www.youtube.com/playli....st?list=PLmMD9No9Nct
Parenting Ideas
https://www.youtube.com/playli....st?list=PLmMD9No9Nct
English Reading Practice
https://www.youtube.com/watch?v=PSdNKSv3mmE&list=PLmMD9No9Nct3vTbNsxm_mINEsftIzW_9l
I Discover!!!
https://youtube.com/playlist?l....ist=PLmMD9No9Nct0buu
Math is Cool!!!
https://www.youtube.com/playli....st?list=PLmMD9No9Nct
Hindi Vyakaran
https://www.youtube.com/playli....st?list=PLmMD9No9Nct
If you like the content, give it a thumbs up, comment and please consider subscribing!!
Disclaimer: Some content is used for educational purpose under fair use. Copyright Disclaimer Under Section 107 of the Copyright Act 1976, allowance is made for ‘fair use’ for purposes such as criticism, comment, news reporting, teaching, scholarship and research. Fair Use is a use permitted by copyright statute that might otherwise be infringing. All credit for copyright material used in video goes to respected owner.
Stay connected:
E-mail- bhavnakeswani_3@yahoo.co.in
Subscribe: www.youtube.com/BhavnaKeswani
#greaterthan #lessthan #equalto #mathiscool
#multiplicationsong #repeatedaddition #mathsong
A Jack Hartmann inspired catchy math song teaching about repeated addition being multiplication 1st 2nd 3rd grade math from Dr. S; a real teacher with a PhD in Education! Add the same number again and again equals the same as multiplication facts double addition facts song
Follow me on instagram!
instagram.com/drskidsmusic
Listen on-
Spotify:
https://open.spotify.com/track..../5jDKVNlb1Ol6LjUpfSq
Apple Music:
https://music.apple.com/us/alb....um/multiplication-my
Lyrics:
7 on me, 7 on you
equals the same as 7 times 2
4 for her, 4 for him, and 4 for me
equals the same as 4 times 3
Add the same number again and again
that is multiplication my friend
9 on me, 9 on you
equals the same as 9 times time
2 for her, 2 for him, and 2 for me
equals the same as 2 times three
Add the same number again and again
that is multiplication my friend
5 + 5 + 5 +5 equals the same as
5 x 4 I surely proclaim
8 + 8 + 8 + 8 equals the same as
8 x 4 that's the name of the game
Background credits:
Blue Background: http://www.freepik.com" Designed by Visnezh / Freepik
Cartoon Girl: [a]https%3A%2F%2Fwww.freepik.com%2Fvectors%2Flittle[/a] Little vector created by freepik - www.freepik.com
Let's make math more exciting by singing this song
You can send or write a comment below for the topics / lessons you want me to teach on my next video.
Follow my FB Page for more questions and suggestions: https://www.facebook.com/MsJessasTutorial
#MATHSONG
#shorts
#SHORTS
Hey!
In this video, we are going to learn 7 Maths Short Tricks in just one video. We have explained different calculation methods which can save a lot of time in exams. In this series of videos, we will give you short tricks of all chapters after completion of this series you will be able to fasten your calculation. Stay connected with Dear Sir and subscribe to our channel to join our short trick army.
Also, share this video among your friends so that you all can practice together. Till that Take Care and Best of Luck.
Watch "WHY" Series Videos:- https://www.youtube.com/watch?v=ynHO5...
Watch Clock Chapter:- https://www.youtube.com/watch?v=FseNK...
Share this video among your friends and do practice because practise makes men perfect.
Join us at Telegram :- https://t.me/officialdearsir
Support us by donating:- https://www.youtube.com/dearsir/join
Multiply Karne ki Japani Trick:- https://www.youtube.com/watch?v=bsArp...
- Learn Tricky Math With Short Trick:- https://www.youtube.com/playlist?list...
- Profit and Loss Short Trick Playlist:- https://www.youtube.com/playlist?list...
- Average Short Tricks in Hindi:- https://www.youtube.com/playlist?list...
Time and Work Short Trick:- https://www.youtube.com/playlist?list...
Follow us at:-
1. Facebook:- https://www.facebook.com/officialdearsir
2. Instagram:-
Dear Sir:- @dearsirofficial or click the link https://www.instagram.com/dearsirofficial
Math Tutor:- @dearsiraadi or https://www.instagram.com/dearsiraadi
3. Telegram:- https://www.t.me/officialdearsir
4. Twitter:- https://twitter.com/officialdearsir
5. Google+ :- https://plus.google.com/1126392149936...
Support us by donating little amount:- https://www.youtube.com/dearsir/join
Don’t forget to suggest our channel to someone who needs it:- https://www.youtube.com/dearsir
Here are Key Moments of the video 👇
00:00 Intro of the Video
01:21 Square Trick 1
04:39 Square Trick 2
07:55 Square Trick 3
10:12 Square Trick 4
11:27 Multiply Trick 5
14:13 Multiply Trick 6
16:13 Multiply Trick 7
18:44 Question with Trick
20:01 Outro
-----Thank You for Watching-----
Team “Dear Sir"
With this mental math trick you will beable to add and subtract in your head rapidly - a critical skill in everyday math. In this video we look at tips on how to do basic addition and subtraction instantly without using a calculator. Fast math is good math!
To donate to the tecmath channel:https://paypal.me/tecmath
To support tecmath on Patreon: https://www.patreon.com/tecmath
To buy tecmath mechandise: https://teespring.com/stores/tecmath-store
Check out Brilliant.org to start learning for free - and be among the first 200 people to sign up to get 20% off your subscription: https://brilliant.org/ThomasFrank
If you want to improve your math skills, you need to do lots of math. But how do you progress when you come across a problem that seems impossible? Well, if summoning the spirit of Jeff Goldblum doesn't work, the tips in this video just might.
My book "10 Steps to Earning Awesome Grades" is completely free, so check it out if you're interested in improving your grades!
http://collegeinfogeek.com/get-better-grades/
Check out our latest podcast episode:
https://www.youtube.com/watch?v=ltKj7833aT8
Tools I mentioned:
WolframAlpha: http://www.wolframalpha.com/
Symbolab: https://www.symbolab.com/
Connect with me:
Twitter ➔ https://twitter.com/tomfrankly
Instagram ➔ https://instagram.com/tomfrankly
----------
Videos you might want to watch next:
How to Learn Faster with the Feynman Technique: https://www.youtube.com/watch?v=_f-qkGJBPts
How to Finish Homework Fast: https://www.youtube.com/watch?v=363GWtra7X8
----------
If you want to get even more strategies and tips on becoming a more productive, successful student, subscribe to my channel right here:
http://buff.ly/1vQP5ar
Background music by Broke for Free: http://freemusicarchive.org/music/Broke_For_Free/
Extension for better control over playback speed (if I'm talking too fast) ➔ https://chrome.google.com/webs....tore/detail/video-sp
~ created by Thomas Frank