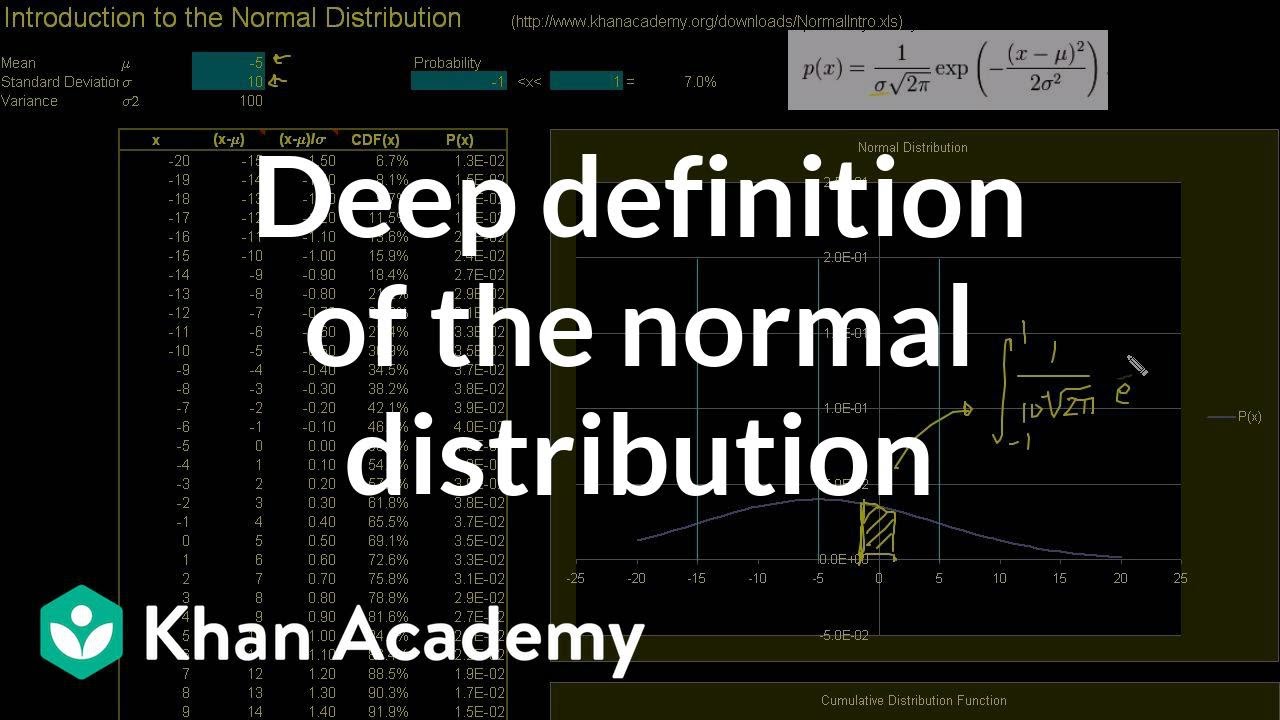
Where 68 - 95 - 99.7 rule comes from (Empirical Rule for Normal Distribution)

When working with a normal distribution you are provided a mean and standard deviation. The empirical rule tells us that there is 68%, 95%, and 99.7% of the normal distribution contained in the first, second, and third standard deviation away from the mean, respectively.

Where do these numbers come from?

In this video, an overview about integrals and the relationship to the standard distribution probability density function provide insight into where these numbers come from.

Some images made using Geogebra.

0:00 What does the empirical rule tell us?
1:05 Normal Distribution probability density function.
1:45 Normal curve with mean of 0 and standard deviation of 1.
2:20 Probability at point vs probability of interval.
2:52 Using integral to calculate area under normal curve.
3:11 Integrals to compute area between standard deviation of the mean for N(0,1) example.
4:29 Setting up table to compare areas for different normal curves.
5:01 How does changing the standard deviation change the spread of the curve?
5:40 Integrals to compute area between standard deviation of the mean for N(0,0.5) example.
6:35 Integrals to compute area between standard deviation of the mean for N(50,10) example.
7:30 Integrals to compute area between standard deviation of the mean for N(1000,25) example.
7:45 Conversation about how area under curve didn't change when varying the mean and standard deviation.
8:12 The empirical rule saves you time from recalculating integrals over and over again.

#68-99-99.7
#empiricalrule
#normaldistribution
#JoeCMath