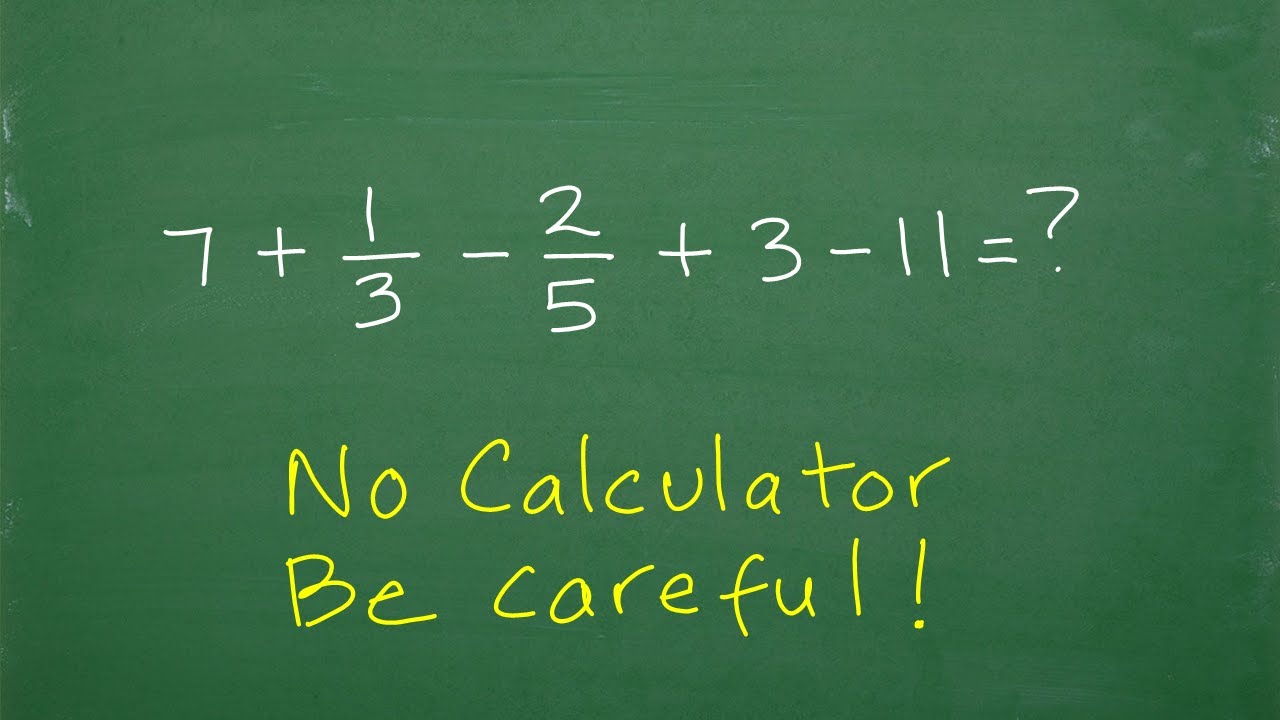Math
Sub Category
Welcome to How to Calculate Sales Tax with Mr. J! Need help with calculating sales tax and total cost? You're in the right place!
Whether you're just starting out, or need a quick refresher, this is the video for you if you're looking for help with sales tax and final price. Mr. J will go through sales tax examples and explain the steps of how to calculate sales tax and final cost.
About Math with Mr. J: This channel offers instructional videos that are directly aligned with math standards. Teachers, parents/guardians, and students from around the world have used this channel to help with math content in many different ways. All material is absolutely free.
Click Here to Subscribe to the Greatest Math Channel On Earth: https://goo.gl/XHTrfY
Follow Mr. J on Twitter: @MrJMath5
Email: math5.mrj@gmail.com
Music: https://www.bensound.com/royalty-free-music
Hopefully this video is what you're looking for when it comes to calculating sales tax and total cost.
Have a great rest of your day and thanks again for watching! ✌️✌️✌️
How to add numbers including fractions and positive and negative numbers.
For more in-depth math help check out my catalog of courses. Every course includes over 275 videos of easy to follow and understand math instruction, with fully explained practice problems and printable worksheets, review notes and quizzes. All courses developed and taught by me (experienced and certified math teacher 🤩).
With my courses you CAN reach your math goal! 💪
All Courses - https://TCMathAcademy.com/
✓Help with Middle and High School Math (Public/Private Schools)
✓High School & College Math Test Prep
✓Teacher Certification Math Test Prep
✓Homeschool Math Program and Courses for Pre-Algebra, Algebra 1, Geometry, Algebra 2 and Pre-Calculus.
TC Math Notes
Pre-Algebra Notes: https://tabletclass-math.creat....or-spring.com/listin
Algebra Notes: https://tabletclass-math.creat....or-spring.com/listin
Geometry Notes: https://tabletclass-math.creat....or-spring.com/listin
Algebra 2 / Trig Notes: https://tabletclass-math.creat....or-spring.com/listin
🚨 NEW MERCH! http://amzn.to/annoyingorange 🚨
➤ Watch more ▸ https://bit.ly/2OWGNhn
➤ AO GAMING CHANNEL! ▸ http://bit.ly/AOGaming
➤ Don't be an apple! Subscribe! It's FREE! ▸ http://bit.ly/AOSub
▾▾▾ More awesome stuff below ▾▾▾
MERCH:
MUSIC!: http://bit.ly/AOMusic
AO TOYS!: http://bit.ly/AOToys
AO COMICS!: http://bit.ly/AOComics
FOLLOW ME:
TWITTER: http://twitter.com/annoyingorange
FACEBOOK: http://facebook.com/annoyingorange
INSTAGRAM: http://instagram.com/annoyingorange
GOOGLE+: http://bit.ly/AOGooglePYouTube
I’m not really a math person…. 😐
Other Socials:
⏰ TikTok: https://www.tiktok.com/@snerixx?lang=en
⏰ 2nd TikTok: https://www.tiktok.com/@samanthaerix?lang=en
📸 Instagram:https://www.instagram.com/snerixx_/
💻 Email: snerixxmanagement@snerixx.com
💌 PO Box: # 48982, Tampa FL 33646
| 𝐁𝐚𝐬𝐢𝐜 𝐌𝐚𝐭𝐡 - 𝐏𝐚𝐫𝐭 𝟏 | 𝐃𝐞𝐟𝐢𝐧𝐢𝐭𝐢𝐨𝐧 : 𝐀𝐝𝐝𝐢𝐭𝐢𝐨𝐧, 𝐒𝐮𝐛𝐭𝐫𝐚𝐜𝐭𝐢𝐨𝐧, 𝐌𝐮𝐥𝐭𝐢𝐩𝐥𝐢𝐜𝐚𝐭𝐢𝐨𝐧 & 𝐃𝐢𝐯𝐢𝐬𝐢𝐨𝐧 | #𝐯𝐢𝐫𝐚𝐥 |
𝐃𝐞𝐟𝐢𝐧𝐢𝐭𝐢𝐨𝐧 : 𝐀𝐝𝐝𝐢𝐭𝐢𝐨𝐧, 𝐒𝐮𝐛𝐭𝐫𝐚𝐜𝐭𝐢𝐨𝐧, 𝐌𝐮𝐥𝐭𝐢𝐩𝐥𝐢𝐜𝐚𝐭𝐢𝐨𝐧 & 𝐃𝐢𝐯𝐢𝐬𝐢𝐨𝐧
𝐃𝐞𝐟𝐢𝐧𝐢𝐭𝐢𝐨𝐧 : 𝐀𝐝𝐝𝐢𝐭𝐢𝐨𝐧
𝐃𝐞𝐟𝐢𝐧𝐢𝐭𝐢𝐨𝐧 : 𝐒𝐮𝐛𝐭𝐫𝐚𝐜𝐭𝐢𝐨𝐧
𝐃𝐞𝐟𝐢𝐧𝐢𝐭𝐢𝐨𝐧 : 𝐌𝐮𝐥𝐭𝐢𝐩𝐥𝐢𝐜𝐚𝐭𝐢𝐨𝐧
𝐃𝐞𝐟𝐢𝐧𝐢𝐭𝐢𝐨𝐧 : 𝐃𝐢𝐯𝐢𝐬𝐢𝐨𝐧
Definition of 𝐀𝐝𝐝𝐢𝐭𝐢𝐨𝐧, 𝐒𝐮𝐛𝐭𝐫𝐚𝐜𝐭𝐢𝐨𝐧, 𝐌𝐮𝐥𝐭𝐢𝐩𝐥𝐢𝐜𝐚𝐭𝐢𝐨𝐧 & 𝐃𝐢𝐯𝐢𝐬𝐢𝐨𝐧
Define 𝐀𝐝𝐝𝐢𝐭𝐢𝐨𝐧, 𝐒𝐮𝐛𝐭𝐫𝐚𝐜𝐭𝐢𝐨𝐧, 𝐌𝐮𝐥𝐭𝐢𝐩𝐥𝐢𝐜𝐚𝐭𝐢𝐨𝐧 & 𝐃𝐢𝐯𝐢𝐬𝐢𝐨𝐧.
#addition #subtraction #multiplication #subtraction #significantdigit #basicoperations #viralvideo2023new #viral #viralvideo #mathshorttrick #mathshorttricks #mathstricks #mathstricks #tipsandtricks #tipsandtrick #trending #trendingvideo
𝐀𝐛𝐨𝐮𝐭 𝐌𝐞 :
I'm a student of 𝐂𝐨𝐦𝐩𝐮𝐭𝐞𝐫 𝐃𝐢𝐩𝐥𝐨𝐦𝐚 in 𝐘𝐂𝐓𝐂 𝐈𝐧𝐬𝐭𝐢𝐭𝐮𝐭𝐢𝐨𝐧 & 𝐁. 𝐓𝐞𝐜𝐡. in 𝐉𝐚𝐝𝐚𝐯𝐩𝐮𝐫 𝐔𝐧𝐢𝐯𝐞𝐫𝐬𝐢𝐭𝐲. I'm in teaching profession for the last 𝟏𝟐 𝐘𝐞𝐚𝐫𝐬.
𝐓𝐞𝐚𝐜𝐡𝐢𝐧𝐠 & 𝐖𝐫𝐢𝐭𝐢𝐧𝐠 are 𝐌𝐲 𝐏𝐚𝐬𝐬𝐢𝐨𝐧.
𝐀𝐛𝐨𝐮𝐭 𝐭𝐡𝐢𝐬 𝐯𝐢𝐝𝐞𝐨 :
This lesson consists of providing you with a Self-Tutorial on all about the BASIC MATHEMATICAL points.
Learn what are "𝐀𝐃𝐃𝐈𝐓𝐈𝐎𝐍, 𝐒𝐔𝐁𝐓𝐑𝐀𝐂𝐓𝐈𝐎𝐍, 𝐌𝐔𝐋𝐓𝐈𝐏𝐋𝐈𝐂𝐀𝐓𝐈𝐎𝐍 & 𝐃𝐈𝐕𝐈𝐒𝐈𝐎𝐍" hope you will like it ...
𝐐𝐮𝐞𝐫𝐢𝐞𝐬 𝐒𝐨𝐥𝐯𝐞𝐝 :
1. What is Mathematics ?
2. What is Significant digit ?
3. How many basic operations of Mathematics ?
4. What is Addition ?
5. What is Subtraction ?
6. What is Multiplication ?
7. What is Subtraction ?
I believe that everyone deserves to learn.
Thank You for watching my video ...
Please comment on below box for your suggestions ....
Don't forget to hit the BELL ICON ...
𝐕𝐢𝐬𝐢𝐭 𝐭𝐡𝐢𝐬 𝐥𝐢𝐧𝐤 𝐢𝐬 𝐟𝐫𝐞𝐞 𝐚𝐧𝐝 𝐏𝐃𝐅 𝐝𝐨𝐰𝐧𝐥𝐨𝐚𝐝𝐬 𝐨𝐟 𝐭𝐡𝐢𝐬 𝐌𝐚𝐭𝐡𝐞𝐦𝐚𝐭𝐢𝐜𝐚𝐥 𝐕𝐢𝐝𝐞𝐨 --
https://drive.google.com/file/....d/1r3PXh3kw7gu3xXvp8
#GenuineFunda #basicmath #education #mathtutorialvideos #mathsclass
class 2 English syllabus :
https://youtu.be/vOh5YhNi18g
2nd class hindi grammar syllabus:
https://youtu.be/37fctYj4gIA
class 2 EVS syllabus :
https://youtu.be/JpiHFMe9gXo
Tens and Ones :
https://youtu.be/ol0CWEojBhQ
Use of was and were:
https://youtu.be/x3fbeqX6BMQ
#class2mathsyllabus
Twitter : https://twitter.com/KidsPride2
Instagram : https://www.instagram.com/1derfulkid/
Youtube : https://www.youtube.com/channe....l/UCvDAstecVtAs85_nY
Linkedin :https://www.linkedin.com/in/kids-pride-63932220b/
Facebook : https://www.facebook.com/kids.pride.180/
Welcome to an “Intro to Evaluating Algebraic Expressions” with Mr. J! Need help with how to evaluate algebraic expressions? You're in the right place!
Whether you're just starting out, or need a quick refresher, this is the video for you if you're looking for help with how to evaluate expressions. Mr. J will go through examples of evaluating expressions with one variable, evaluating expressions with two variables, and explain the steps of how to evaluate an expression.
MORE VIDEOS ON ALGEBRAIC EXPRESSIONS:
✅ Intro to Evaluating Algebraic Expressions = https://youtu.be/k-KiWkV81fQ
✅ How to Evaluate Algebraic Expressions with One Variable = https://youtu.be/Vhrk2iRj6fE
✅ How to Evaluate Algebraic Expressions with Two Variables = https://youtu.be/GheEHcAvdKA
✅ Evaluating Algebraic Expressions with Exponents = https://youtu.be/Fu_TstXlHsE
✅ Evaluating Algebraic Expressions with Variables Next to Each Other = https://youtu.be/DkcU1aWc7Ok
✅ Evaluating Algebraic Expressions in Fractional Form = https://youtu.be/rkNGAQK8jL8
✅ What Does it Mean When a Number is Next to a Variable? = https://youtu.be/XYJSzvgy9zo
About Math with Mr. J: This channel offers instructional videos that are directly aligned with math standards. Teachers, parents/guardians, and students from around the world have used this channel to help with math content in many different ways. All material is absolutely free. #MathWithMrJ
Click Here to Subscribe to the Greatest Math Channel On Earth: https://goo.gl/XHTrfY
Follow Mr. J on Twitter: @MrJMath5
Email: math5.mrj@gmail.com
Music: https://www.bensound.com/royalty-free-music
Hopefully this video is what you're looking for when it comes to evaluating algebraic expressions.
Have a great rest of your day and thanks again for watching! ✌️✌️✌️
✅ Thanks to Aloud, this video has been dubbed into Spanish and Portuguese. #DubbedWithAloud
English
This video has been dubbed into Spanish (United States) and Portuguese (Brazil) using an artificial voice via https://aloud.area120.google.com to increase accessibility. You can change the audio track language in the Settings menu.
Spanish
Este video ha sido doblado al español con voz artificial con https://aloud.area120.google.com para aumentar la accesibilidad. Puede cambiar el idioma de la pista de audio en el menú Configuración.
Portuguese
Este vídeo foi dublado para o português usando uma voz artificial via https://aloud.area120.google.com para melhorar sua acessibilidade. Você pode alterar o idioma do áudio no menu Configurações.
#basicMath, #pvrstudy
#zeroLevelMaths,
#basicGanit,
basic mathema,tics,
basic mathematics topics,
list of basic mathematics topics,
basic mathematics topics for primary school,
basic mathematics topics for entrance exam,
form one basic mathematics topics,
how to learn math,
how to learn maths from the beginning,
how to learn maths from basics,
how to start learning math again,
how to self-study math,
how to study mathematics alone in self-study,
basic maths for beginners
basic classes for 1-10th classes,
learn multiplication tables fast,
zero to hero level maths,
basic maths in hindi,
Simplification Trick |Simplification short trick | math short tricks #shorts #shortvideo #maths
simplification tricks simplification tricks for bank exams
simplification tricks in telugu simplification tricks in tamil simplification tricks adda247 simplification tricks in tamil tnpsc group 4
simplification tricks for tnpsc group 2
simplification tricks by ashish arora
simplification tricks tnpsc tamil
simplification tricks in tamil tnpsc
simplification short tricks simplification short tricks for bank exam
simplification short tricks for bank exams in telugu simplification short tricks tnpsc
simplification short tricks for ssc
simplification short tricks for tnpsc group 4
simplification short tricks by dear sir
simplification short tricks by imran sir
#Simplification #simplificationshorttricks
#simplificationtricks
#ssccgl #sscchsl #sscgd #mathstricks #mathsshorttricks
#vedicmaths
#youtubeshorts
@Maths scam
@Free maths PK
@MATHS KI DUNIYA
@maths masti
@Gagan Pratap Maths
@Dear Sir
@Abhinay Maths
How to Multiply Mixed Numbers? Basic Math Review
Fraction Playlist: https://youtube.com/playlist?l....ist=PL88eWltTZcUYyco
Join our facebook page: www.facebook.com/MathTutorialsforFree
Follow me on my social media accounts:
Youtube: www.youtube.com/c/MathTeacherGon/
Tiktok: https://vt.tiktok.com/ZSdHt9Nt3/
Facebook: www.facebook.com/MathTutorialsforFree
#fractions
#basicmaths
#mathteachergon
#civilserviceexam
learn numbers
learn addition of numbers
mathematical addition of numbers
कक्षा 1 से कक्षा 8 तक के बच्चों को basic से math कैसे सिखाएं || वरदान बैच
#1_se_5_tak_ke_baccho_ko_kaise_पढ़ाये
#chote_baccho_ko_kaise_padhaye
#bache_ko_kaise_padhaye
#tuition_kaise_पढ़ाये
#bacho_ko_padhne_ka_tarika
#bacho_ko_tution_kaise_padhaye
#Ganw_me_coaching_centre
#coaching_mai_kaise_padate_hai
#ghar_pe_kon_sa_business_kre
#grow_your_coaching_classes
#how_to_start_a_coaching_business
#shiksha_niketan_barakar_tundi_dhanbad
#how_to_start_a_coaching_business_from scratch
#grow_your_coaching_business
#how_to_start_a_life_coaching_बिज़नेस
my channel link:-
https://youtube.com/c/MATHCLASSESBYPANKAJSIR
FACEBOOK :https://www.facebook.com/profi....le.php?id=1000830608
telegram link:-
https://t.me/mathclassesbypankajsir
THANKS FOR WATCHING 🙏🙏🙏🙏🙏
Maths Tables Flash Cards | Basic Math | Math TLM | Math Working Model|DIY Flash Cards | Mam Sidra |
In this tutorial you will learn how to make DIY math's tables flash cards step by step.
By this way kids can easily learn tables.
#Mathtables
#Kidsspecialcards
#DIYflashcards
#BasicMath
#MathTLM
#Mathsworkingmodel
#howto
#flashcards
#MamSidra
#SidraMam
BODMAS rule || बोडमास का नियम || Sarlikaran math in hindi || Simplification || bodmas
Equipment used by me👇👇
1) Mic link :- https://amzn.to/3gAjEUL
2) Tripod link :- https://amzn.to/3i9Dp5T
3) Mobile phone link :- https://amzn.to/3Va2cFA
4) Marker link :- https://amzn.to/3XL3iJI
Hi,
I am Suman.Welcome to our channel Study Group 100.
About video:-
इस video में सरलीकरण के सवाल का हल करने का तरीका बताया गया है.
simplify
sarlikaran
bodmas rule
bodmas
bodmas question
bodmas maths
bodmas ka niyam
bodmas ke sawal
bodmas ka sawal
bodmas ke sawal kaise karen
bodmas ka sutra
bodmas ka niyam kya hota hai
bodmas ka sawal kaise hal karen
bodmas kaise banta hai
simplification
simplification tricks
sarlikaran math in hindi
sarlikaran math
sarlikaran math trick
बोडमास का नियम
बोडमास
बोडमास के नियम
बोडमास नियम
सरलीकरण
सरलीकरण मैथ ट्रिक
सरलीकरण गणित
BODMAS | bodmas rule | बोडमास के नियम | simplification | bodmas ka niyam | RULE OF BODMAS | bodmas
#bodmas
#bodmasrule
#bodmaskeniyam
#bodmasquestion
#sarlikaran
#simplification
#simplification_short_trick
#studygroup100
Welcome to How to Solve One-Step Inequalities with Mr. J! Need help with solving inequalites? You're in the right place!
Whether you're just starting out, or need a quick refresher, this is the video for you if you're looking for help with solving one-step inequalities. Mr. J will go through one-step inequality examples and explain the steps of solving one-step inequalities.
✅ Solving One-Step Inequalities | Addition and Subtraction:
https://youtu.be/spRnCq58fUo
✅ Solving One-Step Inequalities | Multiplication and Division:
https://youtu.be/h2Pde3JTZ4g
✅ When to Flip the Inequality Sign:
https://youtu.be/76RZWFrJkg4
✅ Why Do We Flip the Inequality Sign:
https://youtu.be/GgCGLE2gZtk
About Math with Mr. J: This channel offers instructional videos that are directly aligned with math standards. Teachers, parents/guardians, and students from around the world have used this channel to help with math content in many different ways. All material is absolutely free.
Click Here to Subscribe to the Greatest Math Channel On Earth: https://goo.gl/XHTrfY
Follow Mr. J on Twitter: @MrJMath5
Email: math5.mrj@gmail.com
Music: https://www.bensound.com/royalty-free-music
Hopefully this video is what you're looking for when it comes to How to Solve One-Step Inequalities.
A comparison between the old school way of multiplying numbers and new hippie dippy common core way.
Area model video source: https://www.facebook.com/villa....ricaelementaryschool
Welcome to Prime Factorization with Mr. J! Need help with how to find the prime factorization of a number? You're in the right place!
Whether you're just starting out, or need a quick refresher, this is the video for you if you're looking for help with prime factorization. Mr. J will go through prime factorization examples and explain the steps of how to find the prime factorization of a number.
MORE VIDEOS:
✅ Prime and Composite Numbers:
https://youtu.be/ydm2cxacPIM
✅ Need help with another topic?... Just search what topic you are looking for + "with Mr. J" (for example, "adding fractions with Mr. J".
About Math with Mr. J: This channel offers instructional videos that are directly aligned with math standards. Teachers, parents/guardians, and students from around the world have used this channel to help with math content in many different ways. All material is absolutely free.
Click Here to Subscribe to the Greatest Math Channel On Earth: https://goo.gl/XHTrfY
Follow Mr. J on Twitter: @MrJMath5
Email: math5.mrj@gmail.com
Music: https://www.bensound.com/royalty-free-music
Hopefully this video is what you're looking for when it comes to prime factorization.
I-click ang link para sa editable soft copy ng worksheets :)
https://drive.google.com/drive..../folders/18s2J8yUoCb
#Mathematics #Subtraction #Pagbabawas #Bilang1-10 #Educational #Kindergarten
In this video, you will learn how to multiply numbers. Two digit numbers, three digit numbers to two digit numbers.
I'm glad to know your opinions, suggestions and thoughts just comment down below.
---
All music used in this video belongs to its rightful owner.
---
I hope you learned something.
Please don't forget to like and subscribe
Thanks for watching
God bless!
Welcome to Dividing Decimals by Decimals with Mr. J! Need help with how to divide a decimal by a decimal? You're in the right place!
Whether you're just starting out, or need a quick refresher, this is the video for you if you're looking for help with dividing decimals. Mr. J will go through dividing decimals by decimals examples and explain the steps of how to divide a decimal by a decimal.
About Math with Mr. J: This channel offers instructional videos that are directly aligned with math standards. Teachers, parents/guardians, and students from around the world have used this channel to help with math content in many different ways. All material is absolutely free.
Click Here to Subscribe to the Greatest Math Channel On Earth: https://goo.gl/XHTrfY
Follow Mr. J on Twitter: @MrJMath5
Email: math5.mrj@gmail.com
Music: https://www.bensound.com/royalty-free-music
Hopefully this video is what you're looking for when it comes to decimal division (specifically, how to divide decimals by decimals).
Have a great rest of your day and thanks again for watching!