Steps for cloning an animal
How Dolly the sheep was cloned and what we learned.
20 years ago Dolly the step was cloned from two sheets.
Here is how they cloned this sheep.
First, they took cells from the udder of one sheep. They grew these cells in the lab.
Next, they took the egg from another sheep and removed the nucleus.
These stopped cells were fused together and inserted into a female sheep who gave birth.

Keywords: Cloning dolly dolly the sheep
Clone nucleus
human cloning cloned sheep animal cloning embryonic stem cells
cloned animal somatic cell transfer
clone animals identical twins bioethics science ethics
sheep

-~-~~-~~~-~~-~-
Please watch: "Study Skills Teacher's Secret Guide to your Best Grades"
https://www.youtube.com/watch?v=f3bsg8gaSbw
-~-~~-~~~-~~-~-
*
*
For more Life Science videos and summaries see,
http://www.moomoomath.com/Midd....le-School-Science-an

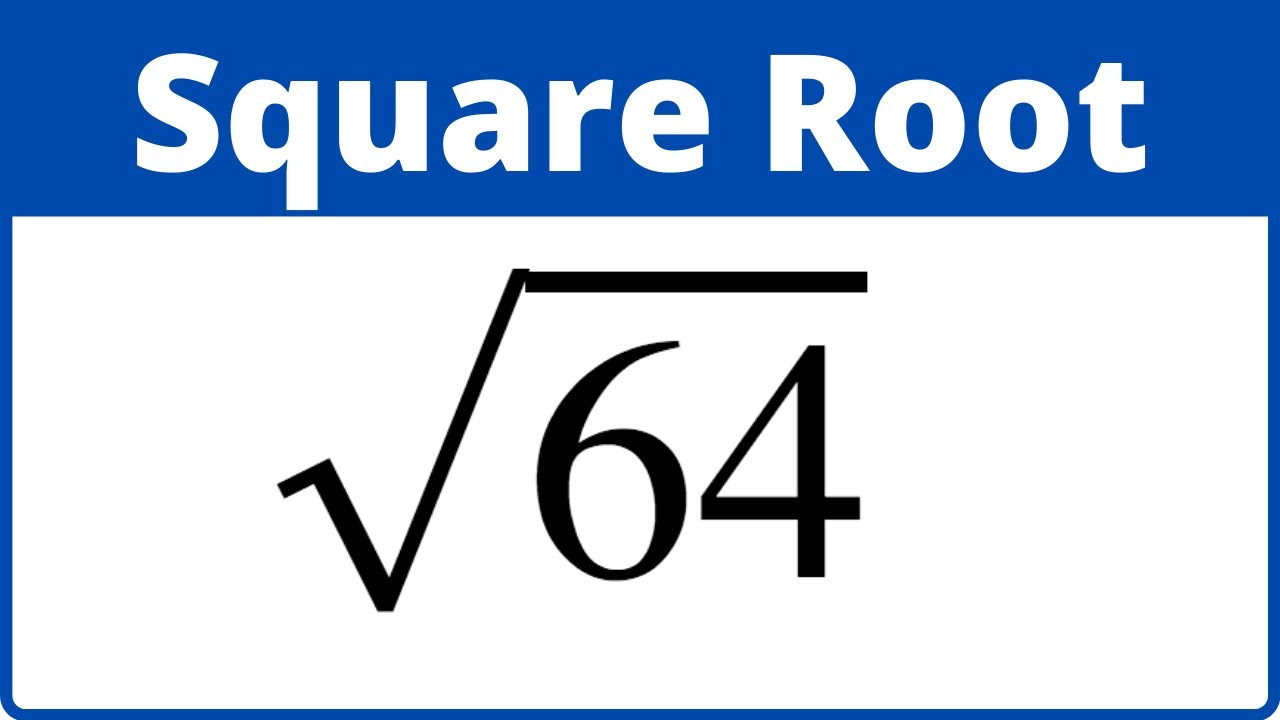
Learn how to find the square root of 64. I like to use a factor tree in order to find all of the prime factors. Then you can pull out pairs of numbers and multiply them together.

In this video I would like to talk about the history of microscopes.During the 1590s, the two spectacle-makers, Hans and Zacharias Jansen began experimenting. They put lenses in a tube and made a very important discovery. They discovered that objects near the end of the tube appeared to be enlarged, much larger than any simple magnifying glass could achieve alone.

In the 1660’s Robert Hooke began looking at all kinds of objects with his microscope.
He put all of his drawings in a book called Micrographia
He is credited with naming cells but also studied items like fleas under his microscope.
Anton van Leeuwenhoek was very good at grinding and polishing lenses.
These lenses led to the building of his microscope which was considered the first practical microscope.
In 1674 Anton Van Leeuwenhoek was the first to see and describe bacteria.
Another huge advance in microscopes didn’t occur until German physicist Ernst Ruska and the electrical engineer Max Knoll constructed the prototype electron microscope in 1931, capable of four-hundred-power magnification.
Electron microscopes uses accelerated electrons in order to view objects.
Modern electron microscopes can magnify objects up to 10 million times

-~-~~-~~~-~~-~-
Please watch: "Study Skills Teacher's Secret Guide to your Best Grades"
https://www.youtube.com/watch?v=f3bsg8gaSbw
-~-~~-~~~-~~-~-
*
*
For more Life Science videos and summaries see,
http://www.moomoomath.com/Midd....le-School-Science-an

An overview of the transition metals. Which group of metals are silver, maybe gold and sometimes liquid? The transition metals
The transition metals are the elements found in groups 3-12.
The transition metals are metallic elements that serve as a bridge, or transition, between the two sides of the table.

You may also enjoy ....
Ions and the PERIODIC TABLE
https://youtu.be/4gT3G6LKYAo

The gas giants which are also called the Jovian planets include the planets, Jupiter, Saturn, Uranus, and Neptune.
These planets are not only huge but have no real surface, are composed of hydrogen and helium, and revolve around the Sun slowly.
These planets also have rings and many moons that revolve around them.

Photo Size of Planets
http://www.lesud.com/lesud-astronomy_pageid81.html

There are four main classifications of galaxies

Elliptical galaxies which are featureless and spiracle.

Galaxy Picture Credits

Spiral galaxy
The Hubble Heritage Team (AURA/STScI/NASA) NASA Headquarters - Greatest Images of NASA (NASA-HQ-GRIN) -http://nix.larc.nasa.gov/info;jsessionid=1sl2so6lc9mab?id=GPN-2000-000933&orgid=12http://imgsrc.hubblesite.org/hu/db/images/hs-1999-25-a-full_tif.tif

Elliptical galaxy

NASA/ESA Hubble Space telescope - http://www.spacetelescope.org/images/potw1519a/

Barred galaxy
NASA, ESA, and The Hubble Heritage Team STScI/AURA) - http://hubblesite.org/newscent....er/archive/releases/ http://www.spacetelescope.org/images/opo0501a/ ([cdn.spacetelescope.org/archives/images/screen/opo0501a.jpg direct link])

Lenticular

NASA, ESA, and The Hubble Heritage Team (STScI/AURA) - http://www.spacetelescope.org/images/opo0624a/ (direct link) http://hubblesite.org/newscent....er/archive/releases/ (direct link)
Spiral these have arms that spiral outward


Lenticular galaxies are given the symbol S0. These galaxies consist of a bright central bulge, similar in appearance to an elliptical galaxy, surrounded by an extended, disk-like structure.

Irregular galaxies are any other galaxy

A concave mirror curves inward in the center. In this video, I use a laser to demonstrate ray of incidence, the ray of reflection,focal point,center of curvature, and the vertex

Learn how to create a stem and leaf plot. A stem and leaf plot is another method for organizing data so you can see patterns.
Draw the Stem and Leaf Chart
Identify the Stem
Sort your data and divide the numbers into a stem and a leaf
Provide a key

Mountain and Valley Breezes occur when the slopes of the mountain and the valley heat up and cool off at different rates. Valley breezes occur during the day and mountain breezes occur at night.

Learn the basics of Lichen and Moss. In many places on Earth, you will find Lichen and Moss living beside each other. Although they may look similar they are very different. Lichen are actually a symbiotic relationship between fungi and cyanobacteria. Moss are nonvascular plants.

Ocean stratification results when ocean water with different densities forms layers due to their properties. In this video, I show how differences in salinity can create ocean stratification which may result in ocean currents.
In the salinity demonstration, I have a container divided into two halves. On one side I have fresh water and the other I have very salty water. The two types of water are separated by a divider. When I lift the divider the salty water flows under the warm water and creates a current.

There are several diferent types of estuaries.
An estuary is a body of water that has fresh water entering and is also open to the ocean. An estuary is a semi-enclosed, coastal body of water, that is connected to the open sea, with fresh water draining into it.
If you look at the state of Georgia you can see the Savannah river run through it. The Savannah river dumps into the Atlantic ocean and creates an estuary. Here is what a small portion of this estuary looks like.

Estuaries are known for their brackish water which is a combination of salt and fresh water. Estuaries have been called the "Nurseries of the Sea." because of the many phytoplankton that is found there help the food chain and provide food for many organisms.

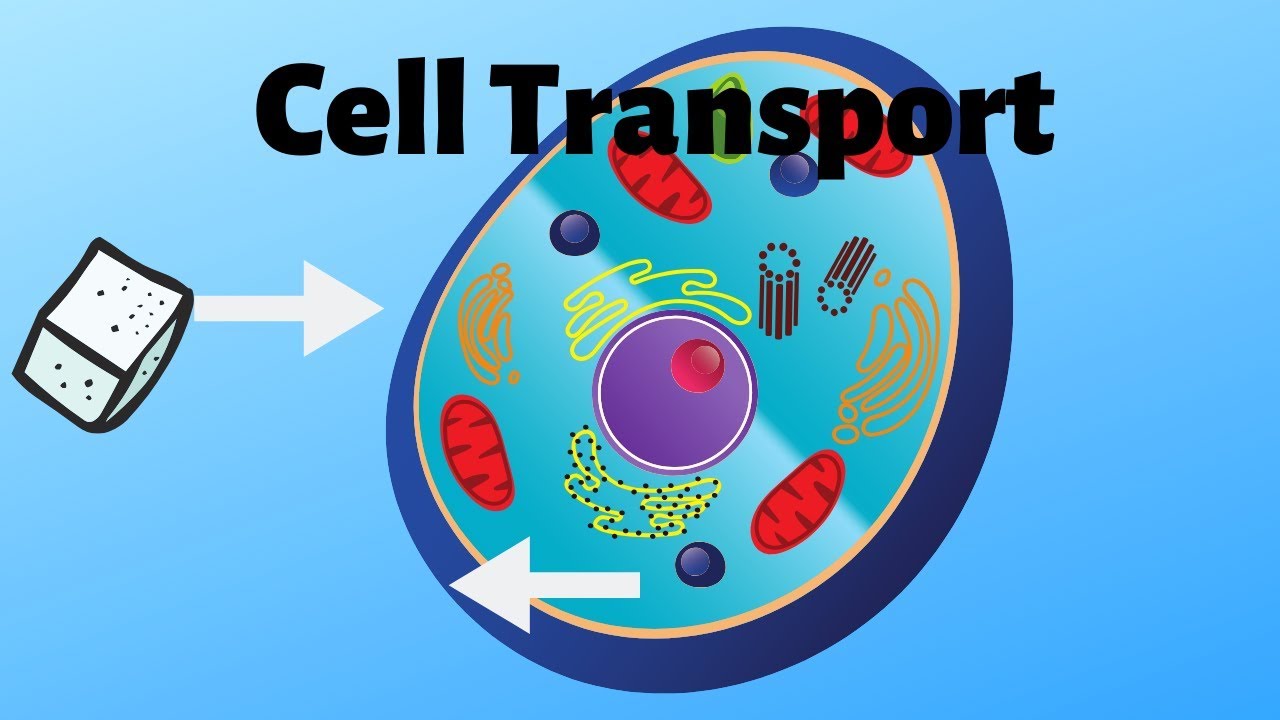
In this video, you will learn about transport across the cell membrane. I cover active and passive transport, diffusion, osmosis, and endocytosis and exocytosis.
Passive transport involves diffusion and osmosis and does not require energy. Objects move from a high concentration to a low concentration.
Active transport requires energy.
I answer questions like, is facilitated diffusion active or passive transport.

In this video, I go through the multiples of 3 up to 20. Knowing the multiples of three and other numbers helps build your number sense.

More information
http://www.moomoomathblog.com/....2022/02/multiples-of

In this video, you will learn about the Circulatory SystemThe circulatory system, is the transportation system of the body and is responsible for the flow of blood in the body. The major structures that make this possible are the heart, blood vessels, and blood.
The heart pumps blood in order to move nutrients oxygen, carbon dioxide disease-fighting white blood cells, and hormones to and from the cells in the body
The circulatory system has two main types of circulation.

The pulmonary
The Systemic
Pulmonary circulation travels from heart to the lung where your blood picks up oxygen and back to the heart
Systemic circulation is from the heart to the body

Your heart has four chambers that is used to pump blood throughout your body.

Two Atria - which are the upper chambers.
Two ventricles - these are the lower chambers
The left and right side of the heart is divided by the septum

Blood Vessels carry blood throughout the body.
Arteries carry blood away from the heart and veins carry blood towards the heart

Capillaries, which are the smallest blood vessels in the body create a network of vessels connecting veins and arteries.
In summary, the heart pumps blood to the body through the arteries and returns blood to the Body through the veins

You have around 1.5 gallons of blood in your body
It is composed of several different types of cells.
The first type of blood cell is the red blood cell. Red blood cells help carry oxygen

The second type of blood cell is known as the white blood cell and helps fight pathogens

The third type of cell is the platelet and create blood clots.
These blood cells are found in a liquid called plasma which consists of water along with electrolytes and some proteins and hormones

In summary, The job of the circulatory system is to circulate blood to and from cells in the body in order to transport nutrients and oxygen and remove carbon dioxide and waste.

MooMooMath uploads a new math and science video every day.
Please subscribe and if you like this video please share it.

I use a factor tree in order to find the cube root of 216.
This video is part of a playlist of finding the cube root of numbers 1 through 50

Learn how to use a factor tree in order to find the lowest common multiple.
I find the LCM of 12 and 15.

Learn the difference between a autotroph and a heterotroph. All plants and other organisms that produce their own food in an ecosystem are called autotrophs. Or self feeders
An Autotrophs is an organism that collects energy from sunlight or inorganic substances to produce food.
A Heterotroph is an organism that gets its energy requirement by consuming other organisms.
They are also called consumers
A heterotroph that eats only planed is called a herbivore
Heterotrophs that eat other heterotrophs are called carnivores. Lions,wolves
An organism that eats plants and animals are omnivores.

More on Autotrophs
http://www.moomoomathblog.com/....2022/05/autotrophs-a

Autotroph and Heterotroph
https://moomoomath.com/autotro....ph-vs-heterotroph-pr

Learn the parts of the microscope and how to focus a compound microscope.
Using a compound microscope can be fun and unlocks a whole new world.
In this video I point out a couple of tips and tricks you can use to help you use a microscope properly.

-~-~~-~~~-~~-~-
Please watch: "Study Skills Teacher's Secret Guide to your Best Grades"
https://www.youtube.com/watch?v=f3bsg8gaSbw
-~-~~-~~~-~~-~-
*
*
For more Life Science videos and summaries see,
http://www.moomoomath.com/Midd....le-School-Science-an

In this video, I cover 3 types of convergent boundaries.
Oceanic and Oceanic, Oceanic and Continental, Continental and Continental lithosphere
I also cover 2 types of divergent boundaries.
Divergent boundaries occur when plate boundaries move away from one another.
Oceanic and Oceanic plus Continental and Continental
Transform boundaries occur when plates move past one another.
More on Plate Boundaries
http://www.moomoomathblog.com/....2021/03/how-tectonic